오늘은 부분 문자열 검색의 부르트포스법, KMP법, 보이어∙무어법에 대해서 공부하려 합니다. :)
부르트포스법은 단순 선형 검색을 확장한 알고리즘으로 단순법이라고 합니다.
이를 응용한 예제 문제를 풀어보겠습니다.
https://www.acmicpc.net/problem/1120
1120번: 문자열
길이가 N으로 같은 문자열 X와 Y가 있을 때, 두 문자열 X와 Y의 차이는 X[i] ≠ Y[i]인 i의 개수이다. 예를 들어, X=”jimin”, Y=”minji”이면, 둘의 차이는 4이다. 두 문자열 A와 B가 주어진다. 이때, A의
www.acmicpc.net
import sys
import heapq
A, B = sys.stdin.readline().strip().split()
def checkGapCount(A, B):
return sum([1 if A[i] != B[i] else 0 for i in range(len(A))])
heap = []
for i in range(len(B) - len(A) + 1):
heapq.heappush(heap, checkGapCount(A, B[i:len(A) + i]))
print(heapq.heappop(heap))1. B문자열을 A문자열 길이 만큼 슬라이싱 합니다.
2. checkGapCount함수를 통해 슬라이싱된 B문자열과 A문자열을 전체 순회하며 차이가 있다면 1 차이가 없으면 0인 배열을 만들어 차이의 값을 모두 더한 값을 return 합니다.
3. heap에 값들을 전부 넣고 마지막으로 heap 에서 최소 값을 꺼내 출력합니다.
행여 값이 들어있는지 확인하고 해당 값의 index를 확인하려면 element in, index() 멤버십 연산자를 사용할 수 있습니다.
** 새로 배운점. 배워야할 점.
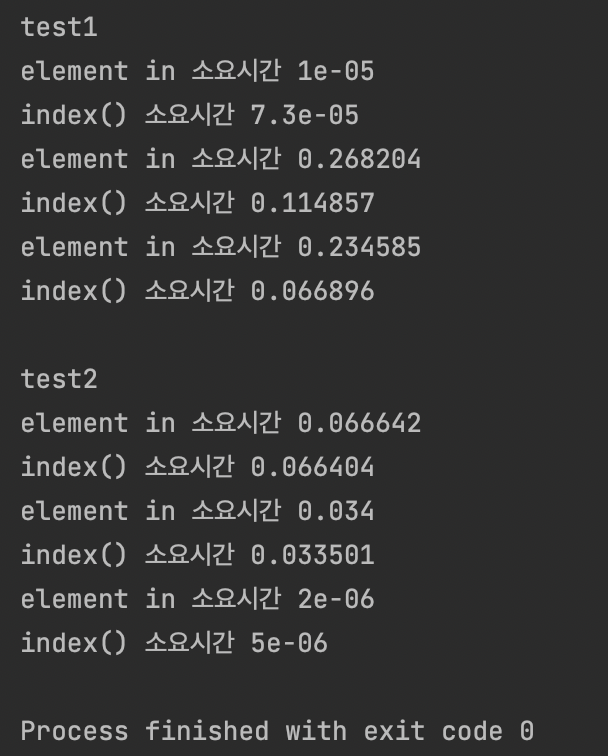
앞선 포스팅에서 element in, index() 모두 O(n) 이여서 O(n ** 2) 시간 복잡를 가질거라 생각했고 연산 시간에 의문이 생겼습니다.
if element in word:
word.index(element)단어길이가 20억인데 element in, index() 모두 생각보다 시간이 오래 걸리지 않았었습니다. 그리고 찾는 단어의 위치가 앞이라면 분명 빨랐지만 가운데 있는 경우와 맨 뒤에 있는 경우, 오히려 맨 뒤에 있는 경우 index를 찾는 시간이 더 빠른 경우도 있었습니다. 아ㅏㅏㅏㅏㅏ...때문에 다음에 document 보고 표준라이브러리를 정리하도록 하겠습니다.
KMP법
브루트포스법과는 다르게 검사한 결과를 사용해 검사한 만큼을 생략하기에 좀더 효율적일 수 있는 알고리즘입니다.
그리고 KMP법인 이유는 만든 사람의 성이 Knuth, Morris, Prett이기 때문이라고 합니다. ( 적당한 예제 문제를 못찾았습니다. )
def kmp_match(txt: str, pat: str) -> int:
pt = 1
pp = 0
skip = [0] * (len(pat) + 1)
skip[pt] = 0
while pt != len(pat):
if pat[pt] == pat[pp]:
pt += 1
pp += 1
skip[pt] = pp
elif pp == 0:
pt += 1
skip[pt] = pp
else:
pp = skip[pp]
pt = pp = 0
while pt != len(txt) and pp != len(pat):
if txt[pt] == pat[pp]:
pt += 1
pp += 1
elif pp == 0:
pt += 1
else:
pp = skip[pp]
return pt - pp if pp == len(pat) else -1다음을 보시면 알겠지만 임의의 skip 배열을 만들고 값을 저장해 그만큼 건너뛰게 됩니다.
보이어∙무어법
보이어∙무어법은 부르트포스법이나 KMP법보다 뛰어난 알고리즘으로 패턴의 끝문자에서 시작해 앞쪽으로 검사를 수행합니다.
그리고 배열 두개를 사용해 임의의 skip 배열을 만들고, KMP와 같이 일치여부를 판단해 검색 과정을 생략할 수 있습니다.
def bm_match(txt:str, pat:str) -> int:
skip = [None] * 256
for pt in range(256):
skip[pt] = len(pat)
for pt in range(len(pat)):
skip[ord(pat[pt])] = len(pat) - pt - 1
while pt < len(txt):
pp = len(pat) - 1
while txt[pt] == pat[pp]:
if pp == 0:
return pt
pt -= 1
pp -= 1
pt += skip[ord(txt[pt])] if skip[ord(txt[pt])] > len(pat) - pp else len(pat)-pp
return -1** 다음 코드는 예제 코드로 배열을 하나만 사용했으며, txt의 길이 제한을 256으로 합니다. **
'자료구조, 알고리즘' 카테고리의 다른 글
| 트리 (1) | 2023.03.08 |
|---|---|
| 리스트 (0) | 2023.03.06 |
| 정렬 알고리즘 - 2 (0) | 2023.02.21 |
| 정렬 알고리즘 - 1 (0) | 2023.02.17 |
| 재귀 알고리즘 (0) | 2023.02.14 |
